GPT4 can play chess
How general are Large Language Model (LLMs) chatbots?
If you're interested in how AI will play out over the next few years, you might care how much "general" intelligence is embedded in these systems. Do they just predict text? Or can they learn to do other interesting things?
Twice today I saw a experts use chess as an example to show that they aren't very general.
In an interview a few weeks ago with Ezra Klein, Demis Hassabis (CEO and co-founder of DeepMind) said:
So if you challenge one of these chat bots to a game, you want to play a game of chess or a game of Go against it, they’re actually all pretty bad at it currently, which is one of the tests I give these chat bots is, can they play a good game and hold the board state in mind? And they can’t really at the moment. They’re not very good.
In a roundtable with Eliezer Yudkowsky and Scott Aaronson, Gary Marcus said:
I would say that the core of artificial general intelligence is the ability to flexibly deal with new problems that you haven’t seen before. The current systems can do that a little bit, but not very well. My typical example of this now is GPT-4. It is exposed to the game of chess, sees lots of games of chess, sees the rules of chess but it never actually figure out the rules of chess. They often make illegal moves and so forth. So it’s in no way a general intelligence that can just pick up new things.
...
I mean, to take the example I just gave you a minute ago, it never learns to play chess even with a huge amount of data. It will play a little bit of chess; it will memorize the openings and be okay for the first 15 moves. But, it gets far enough away from what it’s trained on, and it falls apart.
But they can play chess!
A couple months ago I saw some tweets about how GPT3.5 and GPT4 can play chess if you give it very specialized prompts. (That same account has some other interesting examples showing a "logic core" in GPT.)
That made me curious to try more "normal" prompts, and I found that if you prompt it like this:
Let's play chess. I'll start.
- e4
... and proceed with standard PGN notation, GPT4 makes reasonable, legal moves, even long after the opening.
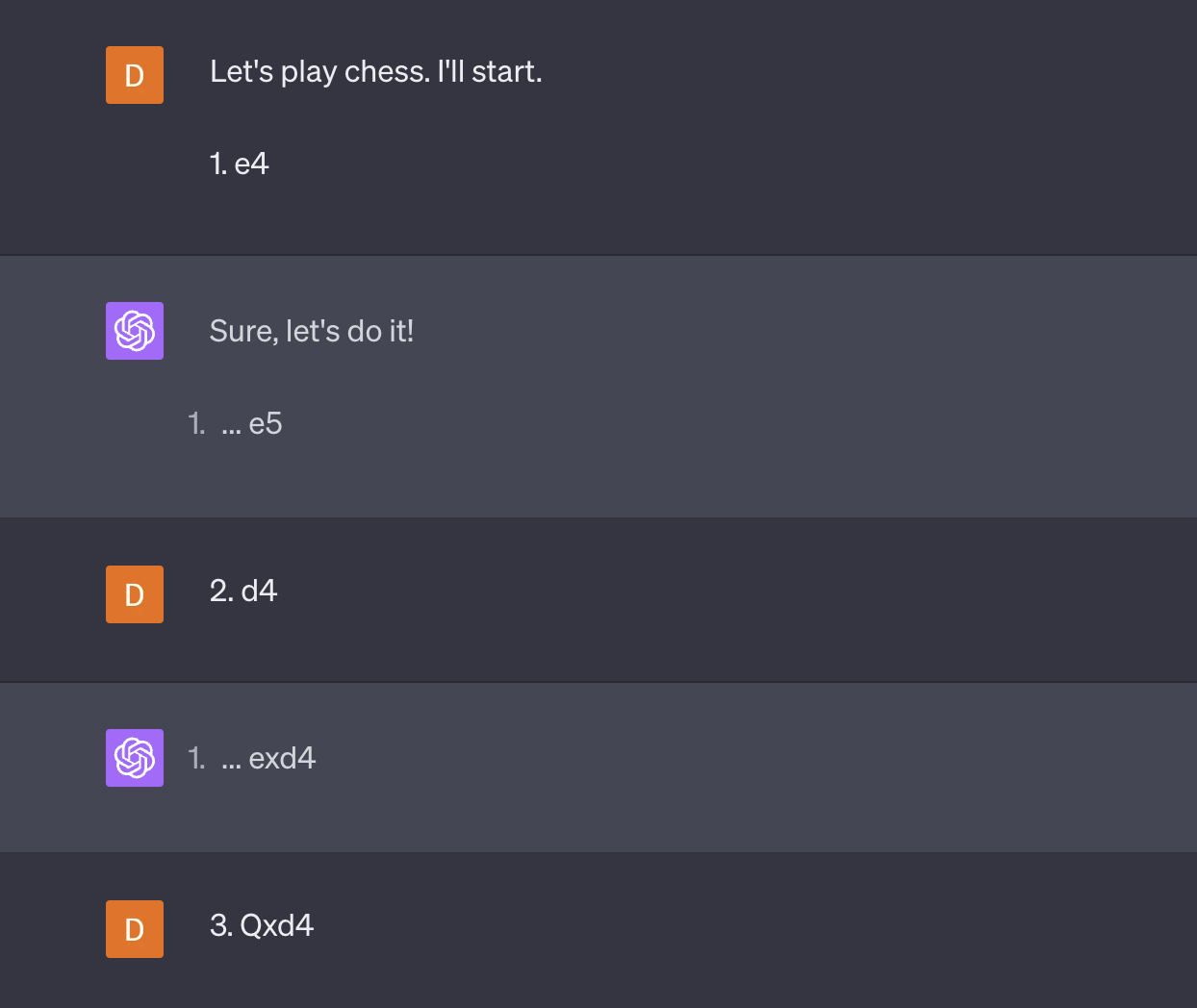
(I don't know why GPT4 is refusing to increment the move numbers with me. When I tried this a couple months ago its move numbers made sense. You'll see in the transcript I got one move number wrong myself.)
I don't know what Demis considers a "good game", but it seems pretty clear to me that GPT4 is able to "hold the board state in mind".
Here's the final position in the game I just played (GPT4 won):
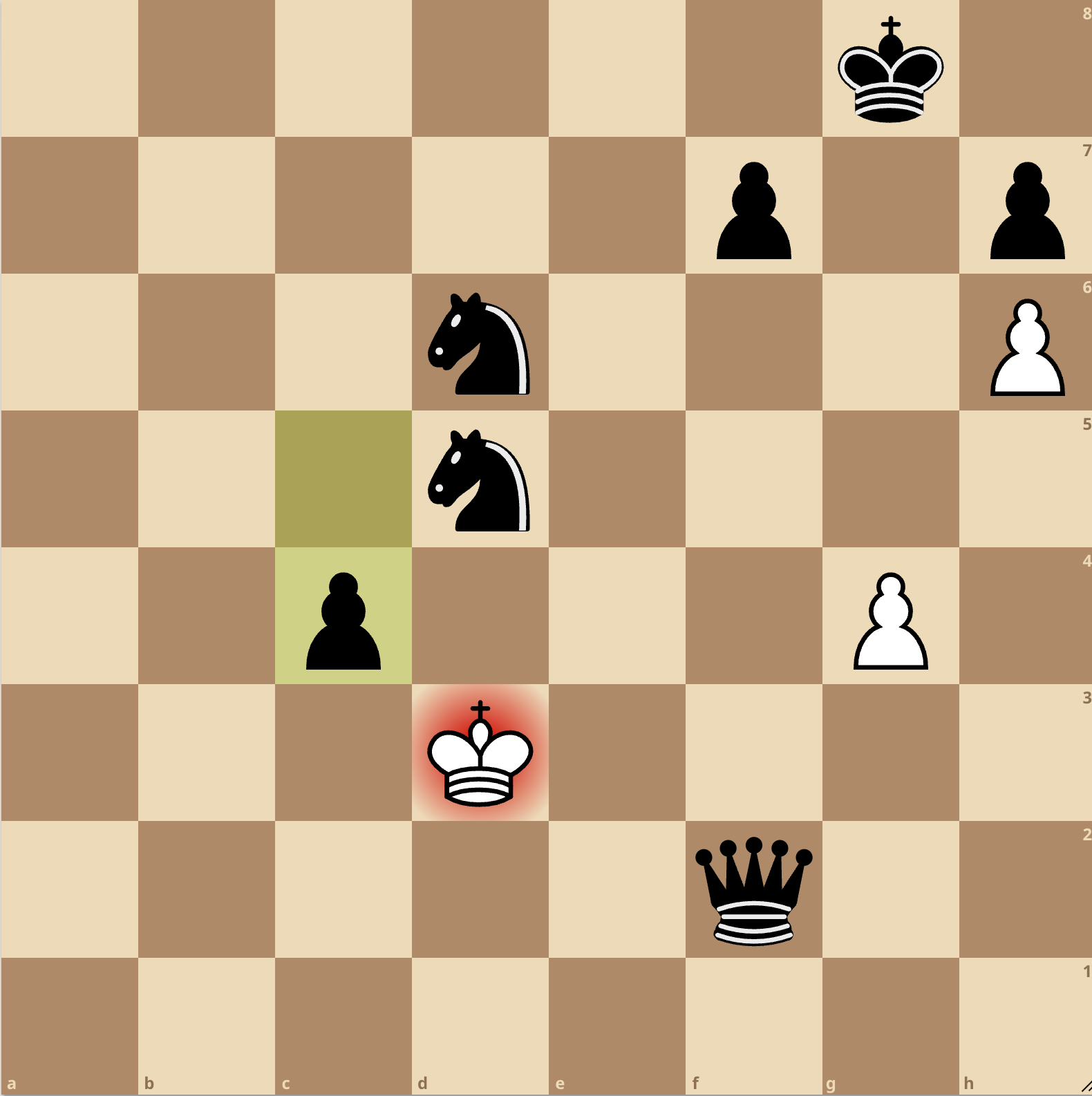
You can see the full transcript here.
To see the full game played out, go to a lichess.org analysis board and paste in the game's PGN notation:
1. e4 e5 2. d4 exd4 3. Qxd4 Nc6 4. Qd1 Nf6 5. Bc4 Bc5 6. b4 Bxb4+ 7. c3 Ba5 8. Nf3 O-O 9. O-O Nxe4 10. Re1 Nf6 11. Qb3 d5 12. Rd1 dxc4 13. Rxd8 cxb3 14. Rxf8+ Kxf8 15. axb3 Bg4 16. Ba3+ Kg8 17. Nbd2 Re8 18. Re1 Rxe1+ 19. Nxe1 Bxc3 20. f3 Bxd2 21. fxg4 Bxe1 22. Kf1 Bb4 23. Bxb4 Nxb4 24. Ke2 c5 25. g5 Ne4 26. h4 b5 27. Ke3 Nd6 28. g4 a5 29. h5 a4 30. bxa4 bxa4 31. h6 gxh6 32. gxh6 a3 33. Kf4 a2 34. Ke3 a1=Q 35. Kf4 Qf6+ 36. Ke3 Nd5+ 37. Kd2 Qf2+ 38. Kd3 c4#
Aside from the move numbers, there's one way in which this record of the game differs from our transcript: On move 17, I said "Nd2", which is an incorrect thing to write, since there are two knights that could move to d2. But GPT4 just went with it, and seems to have correctly figured out which one I meant.
Could this game be memorized?
I can't really prove to you that this game isn't in GPT4's training data, but it seems exceedingly unlikely. I made some intentionally weird moves just to try to get out of any common sequence pretty early.
Is GPT4 good at chess?
This isn't a particularly good chess game, though it's me rather than GPT4 who didn't play very well. I blundered a piece on move 12, and (as mentioned) made a few other intentionally not-good moves.
I don't really know how good GPT4 is at chess. If I can get API access, I'd love to try making a chess bot that could play online.
Why can GPT4 play chess?
I don't work in AI these days, but I'd guess that: GPT4 is trained to predict the text in its training data, and presumably there are a lot of chess games out there on the internet for it to read. By learning the rules of chess and some ability to reason about the board state and good moves, it does a better job predicting those games.
Did I cherry-pick this example? Is this behavior reliable?
First, I even one example like this shows that GPT4 is able to hold the board state in mind. If I'd had to play 100 games where forgot the board position, even one where it tracks the board and plays pretty well is interesting.
But no, I didn't cherry-pick the example. I played a little bit in this format a couple months ago (and I don't think GPT4 made any illegal moves), and then today after seeing these comments that chat bots can't play chess, I tried one and only one game. That's this one. I didn't play any other game for this post, and certainly not any where it made illegal moves and I gave up.
I tried this a couple other times two months ago, but I don't have great data on how often GPT4 is able to complete a game this way.
But it does make illegal moves for some prompts...
Using prompts like the one above seems to work well, but it's true at GPT4 can quickly go off the rails with other prompts.
Here's an example where I asked it to explain its moves, and its 4th move was illegal. That's a big contrast with the above 38-move game where it plays legally the whole time, and wins!
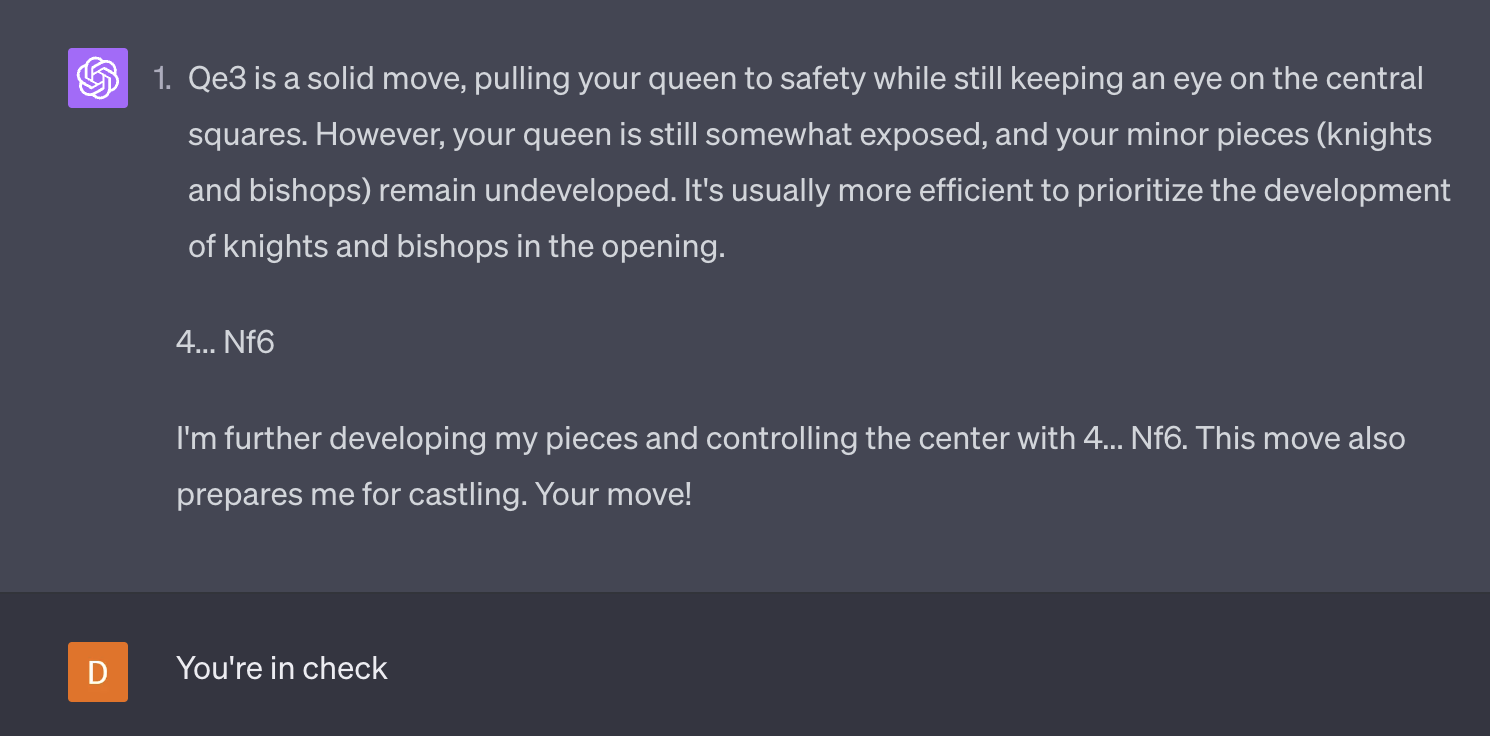
Also here's a chat with the same initial few moves where it plays legally.
Git First-Parent
Messy git history is a display problem, not a data problem.
The first thing I encountered learning about git: there's a lot of conflict about whether it's important to keep a "clean" git history by squashing, rebasing instead of merging, etc. If the --first-parent featue were well supported, it would give us the best of both worlds.
(...click here for the rest of this post)
Regexes for replacing ugly unittest-style assertions
In case they help anyone else, here are some regular expressions I used once to convert some ugly unittest-style assertions (e.g. self.assertEqual(something, something_else) to the pytest style (simply assert something == something_else):
sed -i ".bak" -E 's/self\.assertFalse\((.*)\)/assert not \1/g' tests/*.py
sed -i ".bak" -E 's/self\.assertTrue\((.*)\)/assert \1/g' tests/*.py
sed -i ".bak" -E 's/self\.assertEqual\(([^,]*), (.*)\)$/assert \1 == \2/g' tests/*.py
sed -i ".bak" -E 's/self\.assertIn\(([^,]*), (.*)\)$/assert \1 in \2/g' tests/*.py
sed -i ".bak" -E 's/self\.assertNotEqual\(([^,]*), (.*)\)$/assert \1 != \2/g' tests/*.py
sed -i ".bak" -E 's/self\.assertNotIn\(([^,]*), (.*)\)$/assert \1 not in \2/g' tests/*.py
sed -i ".bak" -E 's/self\.assertIsNone\((.*)\)$/assert \1 is None/g' tests/*.py
sed -i ".bak" -E 's/self\.assertIsNotNone\((.*)\)$/assert \1 is not None/g' tests/*.py
(Pytest gives nice informative error messages even if you just use the prettier form.)
Note:
- The option
-imeans "do it in-place" (modify the file). Including".bak"means "make backups of the old version with this extension". - I don't actually want the backups, but (for some odd reason) on my Mac, not asking for them changed how the regex was interpreted to something that's not right.
- After reviewing and checking in the changes I wanted, I cleaned up the backups with
git clean -f(careful you don't have any unchecked-in changes you want to keep!).
An Interaction or Not? How a few ML Models Generalize to New Data
Source code for this post is here.
This post examines how a few statistical and machine learning models respond to a simple toy example where they're asked to make predictions on new regions of feature space. The key question the models will answer differently is whether there's an "interaction" between two features: does the influence of one feature differ depending on the value of another.
In this case, the data won't provide information about whether there's an interaction or not. Interactions are often real and important, but in many contexts we treat interaction effects as likely to be small (without evidence otherwise). I'll walk through why decision trees and bagged ensembles of decision trees (random forests) can make the opposite assumption: they can strongly prefer an interaction, even when the evidence is equally consistent with including or not including an interaction.
I'll look at point estimates from:
- a linear model
- decision trees and bagged decision trees (random forest), using R's
randomForestpackage - boosted decision trees, using the R's
gbmpackage
I'll also look at two models that capture uncertainty about whether there's an interaction:
- Bayesian linear model with an interaction term
- Bayesian Additive Regression Trees (BART)
BART has the advantage of expressing uncertainty while still being a "machine learning" type model that learns interactions, non-linearities, etc. without the user having to decide which terms to include or the particular functional form.
Whenever possible, I recommend using models like BART that explicitly allow for uncertainty.
The Example
Suppose you're given this data and asked to make a prediction at $X_1 = 0$, $X_2 = 1$ (where there isn't any training data):
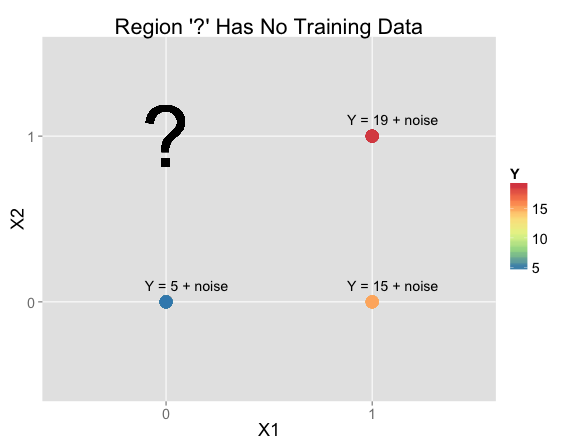
| X1 | X2 | Y | N Training Rows: |
|---|---|---|---|
| 0 | 0 | Y = 5 + noise | 52 |
| 1 | 0 | Y = 15 + noise | 23 |
| 1 | 1 | Y = 19 + noise | 25 |
| 0 | 1 | ? | 0 |
(...click here for the rest of this post)
Covariance As Signed Area Of Rectangles
A colleague at work recently pointed me to a wonderful stats.stackexchange answer with an intuitive explanation of covariance: For each pair of points, draw the rectangle with these points at opposite corners. Treat the rectangle's area as signed, with the same sign as the slope of the line between the two points. If you add up all of the areas, you have the (sample) covariance, up to a constant that depends only on the data set.
Here's an example with 4 points. Each spot on the plot is colored by the sum corresponding to that point. For example, the dark space in the lower left has three "positively" signed rectangles going through it, but for the white space in the middle, one positive and one negative rectangle cancel out.
In this next example, x and y are drawn from independent normals, so we have roughly an even amount of positive and negative:
Formal Explanation
The formal way to speak about multiple draws from a distribution is with a set of independent and identically distributed (i.i.d.) random variables. If we have a random variable X, saying that X1, X2, … are i.i.d means that they are all independent, but follow the same distribution.
(...click here for the rest of this post)
Previous Posts
Simulated Knitting (post) 
I created a KnittedGraph class (subclassing of Python's igraph graph class) with methods corresponding to common operations performed while knitting:
g = KnittedGraph()
g.AddStitches(n)
g.ConnectToZero() # join with the first stitch for a circular shape
g.NewRow() # start a new row of stitches
g.Increase() # two stitches in new row connect to one stitch in old
#(etc.)
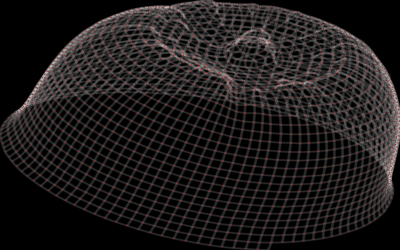
I then embed the graphs in 3D space. Here's a hat I made this way:
2D Embeddings from Unsupervised Random Forests (1, 2) 
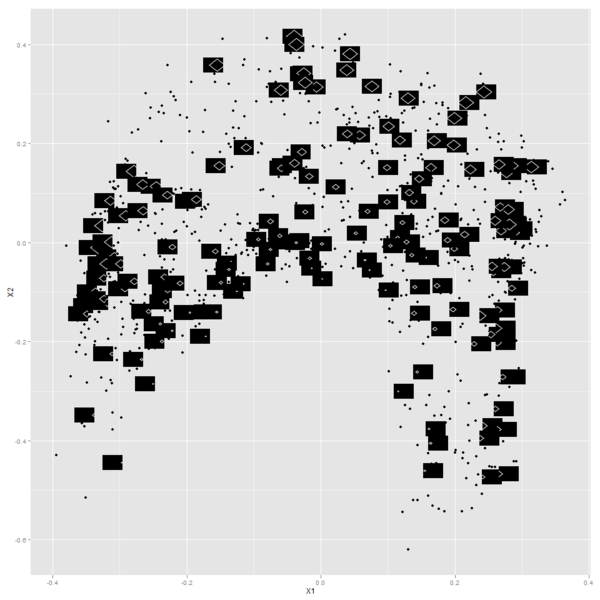
There are all sorts of ways to embed high-dimensional data in low dimensions for visualization. Here's one:
- Given some set of high dimensional examples, build a random forest to distinguish examples from non-examples.
- Assign similarities to pairs of examples based on how often they are in leaf nodes together.
- Map examples to 2D in such a way that similarity decreases decreases with Euclidean 2D distance (I used multidimensional scaling for this).
Here's the result of doing this on a set of diamond shapes I constructed. I like how it turned out:
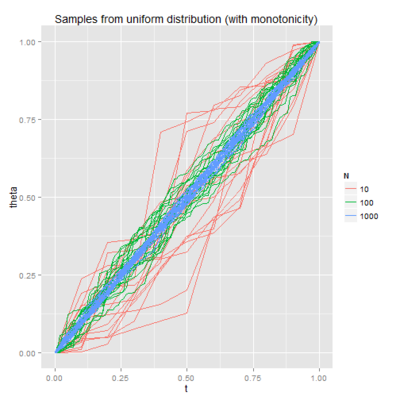
A Bayesian Model for a Function Increasing by Chi-Squared Jumps (in Stan) (post) 
In this paper, Andrew Gelman mentions a neat example where there's a big problem with a naive approach to putting a Bayesian prior on functions that are constrained to be increasing. So I thought about what sort of prior would make sense for such functions, and fit the models in Stan.
I enjoyed Andrew's description of my attempt: "... it has a charming DIY flavor that might make you feel that you too can patch together a model in Stan to do what you need."
Lissijous Curves JSFiddle
Some JavaScript I wrote (using d3) to mimick what an oscilloscope I saw at the Exploratorium was doing:
Visualization of the Weirstrass Elliptic Function as a Sum of Terms
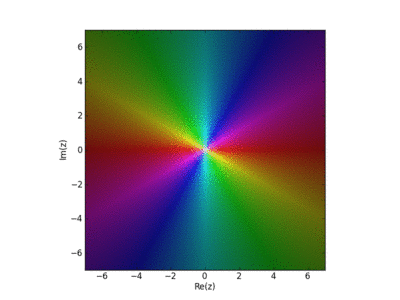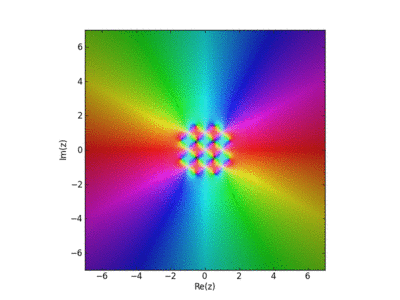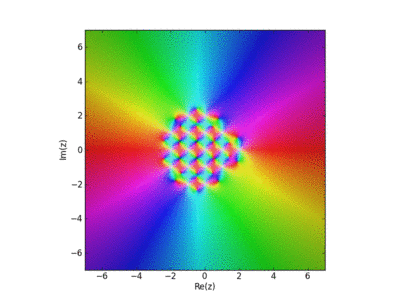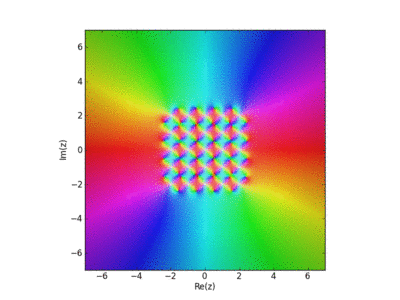
John Baez used this in his AMS blog Visual Insight.
